It’s been almost ten years since I’ve written here. The last time I posted, Donald Trump had just clinched the GOP nomination, his Banzhaf power index had hit 1.0, and I was calculating the proportion of his campaign contributions that were unitemized.¹ That was June 2016. I stopped writing because the general election demanded a firehose of commentary I didn’t have the time or the stomach for, and the opportunity cost of blogging versus finishing actual research was getting untenable.

A lot has happened. Some of the people who used to read this blog — colleagues, friends, people I admired — aren’t here anymore. I won’t make a list, because that isn’t what this space is for, but I’ll say that their absence is felt, and that part of what brings me back is the sense that the kind of work this blog tries to do — taking the math seriously, taking the politics seriously, and refusing to pretend you can do one without the other — matters more now than it did when I left.

For those who are new: this is a blog about the math of politics, which is a thing that exists whether or not anyone writes about it. The tagline is three implies chaos, which is a reference to the fact that collective decision-making with three or more alternatives is, under very general conditions, a mess.² I’m a political scientist at Emory. I use formal models — game theory, mechanism design, social choice — to study how institutions shape behavior. And I write here when something in the news is so perfectly illuminated by the theory that I can’t not.

Today a federal judge ruled that the IRS violated federal law approximately 42,695 times, and I have a model for that. Let’s go.

---

NA NA

Last April, Treasury Secretary Bessent and DHS Secretary Noem signed a memorandum of understanding allowing ICE to submit names and addresses to the IRS for cross-verification against tax records. ICE submitted 1.28 million names. The IRS returned roughly 47,000 matches. The acting IRS commissioner resigned over the agreement. And Judge Colleen Kollar-Kotelly, reviewing the IRS’s own chief risk officer’s declaration, found that in the vast majority of those 47,000 cases, ICE hadn’t even provided a valid address for the person it was looking for — as required by the Internal Revenue Code. The address fields contained entries like “Failed to Provide,” “Unknown Address,” or simply “NA NA.”³

NA NA.

That’s what ICE typed into the field that was supposed to ensure the government could only access tax records for individuals it had already specifically identified. And the IRS said: close enough.

Now, the obvious story here — the one you’ll get from the news — is about a legal violation and an institutional failure. And that story is correct. But there’s a deeper story, one that requires thinking about what classification systems do to the populations they classify. Because the address field in the §6103 request wasn’t just a data element. It was a constraint — a design specification that determined what kind of system the IRS-ICE pipeline would be. With the address requirement enforced, the system is a targeted lookup: you ask about a specific person you’ve already identified, and the IRS confirms or denies. With the address requirement collapsed — with “NA NA” treated as a valid input — the system becomes a dragnet. Same code, same database, same agencies. But a fundamentally different machine, operating under fundamentally different logic, with fundamentally different consequences for the people inside it.

I want to talk about those consequences. Specifically, I want to talk about what happens to the population being classified when the classifier changes.

---

Filing Taxes as a Strategic Choice

Here’s the setup. If you’ve read the work Maggie Penn and I have been doing on classification algorithms, this will look familiar.⁴

Undocumented immigrants in the United States pay taxes. They do this using Individual Taxpayer Identification Numbers (ITINs), which the IRS issues specifically to people who have tax obligations but aren’t eligible for Social Security numbers. Filing is not optional — the legal obligation exists regardless of immigration status. But the compliance rate — how many people actually file — has historically been sustained by a critical institutional feature: a firewall between tax data and immigration enforcement. Section 6103 of the Internal Revenue Code strictly prohibits the IRS from sharing taxpayer information with other agencies except under narrow, court-supervised conditions.

The firewall is what made tax filing a safe act. Filing carried a compliance benefit — potential refunds, building a record for future status adjustment, staying on the right side of the IRS — and essentially zero enforcement cost. The tax system observed you, but the immigration system couldn’t see what the tax system saw.⁵ To put it in terms we’ll use throughout: the classifier’s expected responsiveness was zero.⁶ When the classifier is null, people make their filing decision based solely on the intrinsic costs and benefits of compliance. Call that sincere behavior.

The MOU blew a hole in that firewall. After the MOU, filing generates a signal — the tax record, including your address — that feeds directly into an enforcement match. Before the breach, the only classifier that mattered was the IRS’s own enforcement system, and that system rewarded filing: if you complied, you reduced your probability of audit, penalty, and all the administrative misery that follows from the IRS noticing you didn’t file. The reward was real, the classifier was responsive to compliance, and the equilibrium worked.

The MOU layered a second classifier on top — the ICE match — and this one runs in the opposite direction. Filing still reduces your IRS enforcement risk, but it now increases your immigration enforcement risk, because filing is what generates the data that feeds the match. For citizens and legal residents, the second classifier is irrelevant — they face no immigration enforcement cost, so the net calculus doesn’t change. For undocumented immigrants, the second classifier dominates. The expected cost of filing went up, and for many people it went up enough to swamp the expected benefit.

The equilibrium compliance rate in the model is

$$\pi_F(\delta, \phi, r) = F(r \cdot \rho(\delta, \phi))$$

where $r$ captures the net stakes of being classified and $\rho$ captures how much the classifier’s decision depends on the individual’s behavior.⁶ When the firewall was intact, the net reward to filing was positive — the IRS classifier rewarded compliance, and the immigration system couldn’t see you. When the firewall broke, the net reward dropped, in some cases below zero, and the filing rate dropped with it. Not because the legal obligation changed. Not because the refund got smaller. Because the classifier changed, and people responded.

This is a point that’s worth pausing on, because it’s general and it’s important: classification systems do not passively observe the world. They reshape it. A credit-scoring algorithm changes how people use credit. An auditing algorithm changes how people report income. A policing algorithm changes where people walk. The instrument and the thing being measured are not independent of each other, and any analysis that treats them as independent will be wrong in a specific, predictable direction: it will overestimate the accuracy of the system and underestimate its behavioral effects.

Think of two cities, each with a system for issuing speeding tickets. One city’s algorithm is designed to ticket speeders — it cares about accuracy. The other city’s algorithm is designed to generate revenue — it tickets indiscriminately. Drivers in the accuracy-motivated city slow down, because compliance is rewarded. Drivers in the revenue-motivated city don’t bother, because ticketing has nothing to do with their behavior. Same roads, same drivers, same speed limits. Different classifiers, different equilibria. The classifier doesn’t just measure the city — it makes the city.⁷

---

The Death Spiral

This is where it gets interesting. And by “interesting” I mean “bad.”

The people most likely to be correctly identified by the IRS-ICE match are those with stable addresses who file consistently and accurately. These are, almost by definition, the most compliant members of the undocumented population — the ones who’ve been following the rules, building a paper trail, doing exactly what the system told them to do. They’re also the ones with the most to lose from enforcement, because they’ve given the system the most data about themselves.

These are the first people who stop filing.

Judge Talwani flagged this directly. Community organizations that provide tax assistance to immigrants can’t advise their members to stop filing — that would be encouraging illegal behavior. But they also can’t encourage filing, because filing now triggers enforcement risk. The organizations reported decreased revenue and participation. The chilling effect isn’t hypothetical. It’s in the court record.

Now here’s the feedback loop. When the most identifiable filers exit the system, the quality of the remaining data degrades. The match rate goes down. The false positive rate — the probability that a match incorrectly targets a citizen or legal resident — goes up, both because the denominator of correctly matched records shrinks and because ICE is submitting garbage inputs (“NA NA”) that the IRS is accepting anyway. The classifier gets worse at its stated objective precisely because it’s operating.

The system doesn’t just get unfair. It gets worse at its own stated purpose — identifying specific individuals — because the individuals it could most easily identify are exactly the ones who stop showing up.

This is a general property of classification systems with endogenous behavior, and it’s one I think about a lot. When the population being classified can respond to the classifier, the classifier doesn’t observe a fixed distribution. It selects the distribution that’s willing to be observed. And that selection runs in exactly the wrong direction if your goal is accurate identification: the easy cases exit, the hard cases remain, and accuracy deteriorates as a function of the classifier’s own operation. The system eats its own inputs.⁸

---

What the Designer Wants Matters

One of the results Maggie and I are most insistent about is that the objectives of the entity doing the classifying shape the equilibrium in ways that aren’t obvious from the classifier’s structure alone. Two cities with identical data, identical populations, and identical infrastructure but different objectives will design different classifiers, induce different behavior, and produce different social outcomes. The objectives live inside the algorithm, not alongside it.

So: what is DHS trying to do?

The official framing is accuracy-aligned. DHS says the goal is to “identify who is in our country.” That sounds like accuracy maximization: correctly match individuals to their immigration status.

But the implementation tells a different story. An accuracy-maximizing designer needs good inputs — the whole point of the §6103 requirement that ICE provide a valid address is to ensure the system operates on pre-identified individuals, which is a precondition for accurate matching. ICE submitted “NA NA.” They submitted jail addresses without street locations. They submitted 1.28 million names and got 47,000 matches, meaning a 96.3% non-match rate before you even get to the question of whether the matches were accurate.

This doesn’t look like accuracy maximization. It looks like a fishing expedition — a bulk data pull designed to maximize the reach of the enforcement system rather than the precision of individual identifications. In the language of the paper, it looks more like compliance maximization (or its dark inverse: maximizing the chilling effect on a target population) or outright predatory objectives — a system that benefits from inducing non-compliance, because non-compliance makes the targets more vulnerable, not less.⁹

And the distinction between objectives matters formally, because the two produce different classifiers with different welfare properties. An accuracy-maximizing classifier, we show, will push some groups toward compliance and others away — exacerbating behavioral differences between groups even when the data quality is identical across groups. A compliance-maximizing classifier, by contrast, always satisfies what we call aligned incentives: it pushes all groups in the same behavioral direction.

Here, the groups aren’t abstract. They’re citizens, legal residents, and undocumented immigrants, all of whom file taxes, all of whom had their data swept into the same match, and all of whom face different enforcement costs from being identified. The classifier doesn’t distinguish between them at the input stage — it just matches names and addresses. But the behavioral response to the classifier differs radically across groups, because the stakes of being classified differ radically. Citizens face essentially zero enforcement cost from a match. Undocumented immigrants face deportation. The same classifier, applied to the same data, produces wildly different equilibrium behavior in different populations.

That’s not a bug in the implementation. That’s a structural property of classification systems with heterogeneous stakes. And it’s a property that accuracy maximization makes worse, not better.

---

The Commitment Problem

There’s one more piece of the model that’s eerily relevant. We distinguish between designers who can commit to a classification algorithm and designers who are subject to audit — who must classify consistently with Bayes’s rule and their stated objectives. The commitment case is more powerful: a designer who can commit can deliberately misclassify some individuals to manipulate aggregate behavior. The no-commitment case, which we interpret as the effect of auditing or judicial review, strips away this power.

Judge Kollar-Kotelly’s ruling is an audit. She looked at what the IRS actually did — accepted “NA NA” as a valid address, disclosed 42,695 records in violation of the statutory requirement — and said: this doesn’t satisfy the constraints. Judge Talwani’s injunction goes further, blocking enforcement use of the data entirely.

These rulings function exactly as the no-commitment constraint does in the model. They force the classifier to satisfy sequential rationality — to justify each classification decision on its own terms, rather than as part of a bulk strategy to influence population behavior. And the paper tells us what happens when you impose that constraint: the resulting equilibrium satisfies aligned incentives. The designer can no longer push different groups in different behavioral directions.

That’s the fairness argument for judicial review of classification systems, stated formally. It’s not that judges know better than agencies how to design algorithms. It’s that the constraint of having to justify individual decisions prevents the designer from using the algorithm to strategically manipulate aggregate behavior. The cost is accuracy — the no-commitment equilibrium is always weakly less accurate than what the designer could achieve with commitment power. But the benefit is behavioral neutrality across groups, which is a fairness property that accuracy maximization cannot guarantee.¹⁰

---

Where This Goes

The D.C. Circuit will rule on the Kollar-Kotelly injunction. If they uphold it, the no-commitment constraint holds and the data-sharing agreement is dead in its current form. If they reverse — and the Edwards panel’s reasoning from two days ago suggests this is possible — the commitment case reasserts itself, and the behavioral distortions I’ve described become the operating equilibrium.

Meanwhile, the chilling effect is already in motion. People have already stopped filing. Community organizations have already seen decreased participation. The equilibrium is shifting in real time, and it won’t shift back quickly even if the courts ultimately block the agreement, because trust in the firewall is not a switch you can flip. It’s a belief about institutional behavior, and beliefs update slowly after violations — especially violations that occurred 42,695 times.

The tax system was designed as a compliance mechanism: file your returns, pay what you owe, and we won’t use your data against you. That design was a choice. The firewall was a choice. The address requirement in §6103 was a choice. Every one of those choices encoded a judgment about what the system should be for — not just what it should measure, but what kind of behavior it should sustain. The MOU didn’t just breach a legal firewall. It changed the classifier, which changed the equilibrium, which is changing the population, which will change the data, which will change what the classifier can do. The whole thing is a loop, and it’s spinning in exactly the direction the model predicts.

I said I’d be back when something in the news was so perfectly illuminated by the theory that I couldn’t not write about it. This is that. There will be more.¹¹

With that, I leave you with this.

---

^{1. 72.9%, for those keeping score. ↩}

^{2. The phrase is from Li and Yorke’s 1975 paper “Period Three Implies Chaos,” which proved that a continuous map with a periodic point of period 3 has periodic points of every period — plus an uncountable mess of aperiodic orbits. But the tagline does triple duty: Arrow’s theorem, the Gibbard-Satterthwaite theorem, and the McKelvey-Schofield chaos theorem all say that with three or more alternatives, the relationship between individual preferences and collective outcomes becomes fundamentally unstable. Norman Schofield, who proved the general form of the chaos result with Richard McKelvey, was a mentor and colleague to both Maggie Penn and me at Washington University. It was Norman, in a bar in Barcelona, who suggested that Maggie and I write our first book, Social Choice and Legitimacy: The Possibilities of Impossibility, which we dedicated in part to McKelvey. He died in 2018, and he is one of the people I miss when I write here. Three implies chaos. It’s not a bug. It is the central fact of democratic life. ↩}

^{3. The legal landscape is, to use a technical term, a mess. Kollar-Kotelly’s injunction from November is still in effect but under appeal in the D.C. Circuit. Judge Talwani in Massachusetts issued a separate injunction in early February blocking enforcement use of the data. And two days ago, a D.C. Circuit panel declined to enjoin the agreement, reasoning that “last known address” isn’t protected return information under §6103. So you have district courts saying it’s illegal and an appellate panel suggesting it might not be. Three courts, three bins for the same data. If that doesn’t sound like a social choice problem to you, you haven’t been reading this blog long enough. ↩}

^{4. Penn and Patty, “Classification Algorithms and Social Outcomes,” American Journal of Political Science (forthcoming). The formal model and all the results I’m drawing on here are in that paper. What follows is a blog-post-grade application of the framework, not a formal extension of it. But the shoe fits disturbingly well. ↩}

^{5. The firewall wasn’t just a policy preference — it was constitutional load-bearing infrastructure. The government’s power to tax illegal income was established in United States v. Sullivan (1927) and famously applied to convict Al Capone in 1931. But requiring people to report illegal income creates an obvious Fifth Amendment problem: filing becomes compelled self-incrimination. Section 6103 resolved the tension by ensuring tax data stayed behind the wall. With the firewall intact, you could — in principle — write “narco drug lord” in the occupation field of a 1040 and nothing would happen, because the IRS couldn’t share it. The MOU reopened that wound. If filing now feeds ICE, then filing is self-incrimination for undocumented immigrants, and the constitutional bargain that made the whole system work since Sullivan is back in play. Whether anyone is litigating this yet is a question I leave open, but the logical structure is Gödelian: the system simultaneously compels disclosure and punishes the act of disclosing. ↩}

^{6. In the model, expected responsiveness is $\rho(\delta, \phi) = (\delta_1 + \delta_0 – 1)(2\phi – 1)$, where $\delta_1$ and $\delta_0$ are the probabilities that the classifier’s decision matches the signal for compliers and non-compliers respectively, and $\phi$ is signal accuracy. A null classifier has $\rho = 0$: the probability of being targeted is the same regardless of whether you file. The §6103 firewall enforced nullity by severing the link between the signal (tax record) and the decision (enforcement action). ↩}

^{7. This example is from the paper, but it’s the kind of thing that should be folklore by now. It isn’t, largely because the computer science literature on algorithmic fairness has mostly treated the classified population as fixed. That’s starting to change — see Perdomo et al. (2020) on performative prediction and Hardt et al. (2016) on equality of opportunity — but the political science framing, where the designer has objectives and the population has strategic responses, is still underdeveloped. Maggie and I are trying to fix that. ↩}

^{8. There’s also a revenue dimension that shouldn’t be ignored. The IRS estimates that undocumented immigrants pay billions in federal taxes annually. If the filing rate drops — which it will, and which the court record suggests it already is — that’s tax revenue the government doesn’t collect. The classifier was supposed to serve immigration enforcement, but its equilibrium effect includes degrading the tax base. Whether anyone in the administration has done this calculation is an exercise I leave to the reader. ↩}

^{9. Predatory preferences in the model are characterized by a designer whose most-preferred outcome is to not reward an individual who didn’t comply. Think predatory lending: the lender benefits most when the borrower defaults, because the default triggers fees, repossession, or refinancing at worse terms. A designer with predatory preferences over immigration enforcement would want undocumented immigrants to stop filing taxes, because non-filers are more legally precarious, have weaker paper trails, and are easier to deport. Whether this is what DHS actually wants is a question I can’t answer from the model. But the model can tell you what the observable signatures of predatory preferences look like, and “submit NA NA as an address for 1.28 million people” is consistent with the signature. ↩}

^{10. Whether you think that tradeoff is worth it depends on what you think “fairness” means in this context, and reasonable people disagree. But the point is that it is a tradeoff, with formal properties that can be characterized — not a vague gesture at competing values. I have more to say about this, and about how it connects to a set of problems that go well beyond tax data. But that will have to wait for another post. Or, you know, the book. ↩}

^{11. Next up: the Supreme Court just handed us a game-theoretic goldmine, and three implies chaos. Stay tuned. ↩}

Much has been made today of Donald Trump’s lackluster fundraising productivity in May. I’m going to pile on here, because his campaign is an absolute fiasco in essentially every sense.

In lieu of a full analysis of what this means in terms of inference and prediction, here are three simple rankings/comparisons.  (For the full read of the data, see here: Bernie, Hillary, Trump.)

Total contributions, through the entire cycle through May:

1. Bernie: $224 Million.
2. Hillary: $207 Million.
3. Donald: $17 Million.

Candidates can loan money to their own campaign (meaning they can use campaign contributions to pay themselves back):

1. Donald: $45 Million.
2. Hillary: $0.
3. Bernie: $0.

Third, donations to federal campaigns fall into two categories: itemized and unitemized.  Itemized donations are those that, in sum, for an individual, exceed $200.  Unitemized are those that sum to less than $200 for the donor.

With that said, the proportion of donations that are unitemized to date for each candidate:

1. Donald: 72.9%
2. Bernie: 59.0%
3. Hillary: 21.6%

What does this indicate?

First, Bernie and Hillary are vastly outperforming Trump in terms of raising money.  VASTLY. There’s a bit of chicken and egg here, but the simple fact is that raising money requires a ground operation, and the data confirms observation that Hillary and Bernie have such operations in place, and Trump—well, not so much.

Second, Donald Trump is actually self-financing his campgin on the idea that he will get sufficient contributions to pay himself back.  Hillary and Bernie are not doing so.

Third, Hillary’s contributions are coming from “big” donors much more than are Donald’s (limited) contributions or Bernie’s (significant) contributions.  For Bernie, this makes sense: he is appealing to a swath of the US electorate that doesn’t generally have the wherewithal to donate $200 to a political campaign.

For Trump, maybe the same argument applies…Don’t know.  It’s just a very large ratio of unitemized contributions.  I’ll leave it there.

With this, and in light of the absolutely shameful failure of the Senate to undertake serious efforts at preventing gun violence yesterday, I leave you with this.

The Republican Party is in crisis. This year’s presidential campaign is arguably evidence enough for this conclusion, but it is important to remember that there are really (at least) two “Republican Parties”: one composed of voters and another composed of Members of Congress.

A split in the broader GOP is troublesome for Republican elites because, among other things, it complicates the quest for the White House, which might also cause significant problems for Republican Members seeking reelection. But splits in the broader party do not necessarily affect governing. A split in the “party in Congress,” however, can greatly complicate governing. Indeed, one might argue that the beginnings of such a split caused the downfall of former Speaker Boehner, the government shutdown of 2013, and the near-shutdown of 2015.

As Keith Poole eloquently notes, the potential split in the GOP appears eerily similar to the collapse of the Whig Party in the early 1850s (the last time a major party split occurred in the United States). A key difference between the current Congress and those in the 1850s is the lack of a “second dimension” of roll call voting. Without going into the weeds too much, what this means is that there is no systematic splitting of the Republican party on a repeatedly revisited issue. In the 1850s, that issue was slavery (specifically how it would be dealt with as the nation admitted new states).

Because of this, our roll call-based estimates of Members’ ideologies essentially place all members on a single, left-right dimension. This implies that, for most contested roll call votes, most of the Republicans vote one way and most of the Democrats vote the other. The figure below, which displays the proportion of roll call votes in each Congress and chamber that pitted a majority of one party against a majority of the other, illustrates how this has become increasingly the case.

Of note in the figure are two things. The first is the overall increase in party line voting since the civil rights era. Party line voting was rare during this era in part because the Republican party controlled relatively few seats in either chamber and, relatedly, because the Democratic party often split on civil rights legislation, with Southern Democrats relatively frequently voting with Republicans. As the South “realigned,” beginning in earnest with the 1980 election, the parties became more clearly sorted and party line voting became more common: with civil rights legislation largely off the table, fewer and fewer votes split either party.

The second thing to note is that party line voting dropped precipitously in 1997 (the first Congress of Bill Clinton’s second term), rose during George W Bush’s presidency, and unevenly surged during Obama’s first 3 Congresses. Thus, “partisan voting” is definitely not on the decline in recent years.  This is important for many reasons, but for our purposes it is important because it implies that the nature of “partisan warfare” has not qualitatively changed in terms of the structure of roll call voting, writ large.

Unpredictability and Ideology

Given a Member’s estimated ideology (“ideal point”), we can predict how that member should have voted on each roll call vote. (I am omitting some details.) Using this and the actual votes, we can calculate how many times each Member’s vote was “mispredicted” by the estimated ideal point.

In a nutshell, these are situations in which most of the other Members who have similar ideological voting records voted (say) “Yea,” members on the other side of the ideological spectrum voted “Nay” and the member in question voted “Nay.” For example, if all of the Democrats voted “Nay” on some roll call, and all of the Republicans other than Ted Cruz voted Yea, then Senator Cruz’s vote would be mispredicted by Cruz’s estimated ideal point (which is the most conservative among the current Senate).

Typically, this misprediction, or “error” rate is higher for Members who are (estimated to be) ideological moderates. This is for several reasons. First, if a member is simply voting randomly, then he or she would be estimated to be a moderate. Second, and more substantively, if a member is actually moderate, then his or her vote is more likely to be determined by non-ideological factors because his or her ideological preferences are relatively weaker than for someone who is ideologically extreme.

In any event, the figures below illustrate the House and Senate for a “typical” recent Congress, the 109^th Congress (2005-6). In the 109^th both chambers of Congress were controlled by the Republican Party, following the reelection of George W. Bush. In both figures, the horizontal axis is the estimated ideology so dots on the left represent liberals and dots on the right represent conservative), and the vertical axis is the proportion of votes cast by that member that were mispredicted by his or her estimated ideology. Each figure includes an estimated quadratic equation for “expected error rate.”[1]

 

In both figures, with one notable exception in the 109^th House (Ron Paul (R, TX), Senator Rand Paul’s father), bear out the general tendency for moderates to have higher error rates than “strong” liberals and conservatives. [2]

What About Today? Let’s turn to the 114^th Congress (through March 2016). Looking first at the House, the pattern from the 109^th is still present.[3] Moderates are characterized by higher error rates than strong liberals or conservatives.

In the 114^th Senate (through March 2016), however, the picture is qualitatively and statistically different:
In particular, the Republican party has generally higher error rates than does the Democratic party.[5] This indicates that Republican Senators have been more likely to vote against their party than have been Democratic Senators or, more substantively, the internal ideological structure of the Republican party in the Senate has played a smaller role in determining how GOP Senators have voted in this Congress.

Who’s Being Unpredictable?

Consider the list of the 15 Senators with the highest error rates:

Name	State	Error Rate	Party	Conservative Rank
PAUL	Kentucky	21.2%	GOP	3rd
COLLINS	Maine	20.8%	GOP	54th
MANCHIN	West Virginia	18.1%	Dem	55th
HELLER	Nevada	17.7%	GOP	29th
FLAKE	Arizona	15.7%	GOP	4th
KING	Maine	15.3%	Independent	60th
CRUZ	Texas	15.1%	GOP	1st
KIRK	Illinois	15.0%	GOP	51st
LEE	Utah	14.9%	GOP	2nd
MURKOWSKI	Alaska	13.6%	GOP	53rd
NELSON	Florida	13.4%	Dem	61st
PORTMAN	Ohio	13.2%	GOP	44th
MORAN	Kansas	13.1%	GOP	38th
MCCONNELL	Kentucky	13.0%	GOP	37th
AYOTTE	New Hampshire	12.4%	GOP	46th
HEITKAMP	North Dakota	12.4%	Dem	58th
MCCAIN	Arizona	12.4%	GOP	43rd
GARDNER	Colorado	11.3%	GOP	26th
GRASSLEY	Iowa	11.1%	GOP	48th
CORKER	Tennessee	11.1%	GOP	41st

Tellingly, the four most conservative Senators have incredibly high error rates (and two of these (Paul and Cruz) made serious runs for the GOP presidential nomination). The rest of the list is dominated by Republicans. The four non-GOP Senators are in fairly conservative states (with Maine being an unusual case).[6]

Hindsight and looking back… I don’t have time to get into the weeds even more with this at this moment. For now, I just wanted to point out that voting in the current Senate is unusual: Republicans are breaking with their party more often than are Democrats, and a handful of “extreme” conservatives are breaking with the party at incredibly (indeed, historically) high rates. To quickly see the recent past, consider the 113^th Congress:

In the last Congress, Republicans were already breaking with their party at qualitatively higher rates than were their Democratic counterparts, but there was no real analogue to the cluster of 4 extremely conservative Senators who have been mispredicted so strongly in the 114^th Congress. One of those 4—Senator Flake (R, AZ) was a newly-arrived freshman Senator in the 113^th Congress and has continued to be difficult to predict in his second Congress.

What does it mean? 

In line with both Keith Poole’s conclusion that the GOP shows significant signs of breaking up and the recent revolt among the GOP members in the House (where agenda setting is much more tightly centralized), I think what is happening is that (some of) the “estimated as conservative” wing of the GOP in the Senate is increasingly breaking party lines in pursuit of issues that are not being addressed by the chamber. Qualitative examples of such behavior are seen in the recurrent obstructionism among the “Tea Party wing” of the Republican party. (For example, see my theoretical work on this type of behavior and its electoral origins.) This rhetoric has also flared in the race for (both parties’) presidential nominations.

In line with this, of course, is the fact that the GOP has a disproportionately large number of Senators up for reelection in 2016. I haven’t had time to go through and compare the list of highly mispredicted Senators (please feel free to do so and email me about it!), but my hunch is that a bunch of “in-cycle” Senators are on that list.

For now, though, I leave you with this and this.

________________

 

[1] The quadratic term is significant (and obviously negative) in both chambers, as typical.

[2] The other Members with similarly high error rates in the House are Gene Taylor (D, MS), who would go on to be defeated 4 years later in the 2010 election, and Walter Jones (R, NC), who will show up again below: both were considered “mavericks” and were, as a result, estimated as being relatively moderate in ideological terms. In the Senate, the three highest error rates were (in order) Senator Mike DeWine (R, OH), who would be defeated in the 2006 midterm election by Sherrod Brown, Senator Arlen Specter (R, PA), a moderate Republican, and Senator John McCain (R, AZ).

[3] The quadratic term for the estimation of the relationship between estimated ideal point and error rate is again significant and of course negative.

[4] The quadratic term in this case is still negative, but no longer statistically significant. The linear term is positive, of course, and statistically significant.

[5] As is common in recent Congresses, there is no overlap between the parties’ ideological estimates so far this Congress: Senator Joe Manchin (D, WV) is the most conservative Democratic Senator, and Senator Susan Collins (R, ME) is the most liberal Republican Senator, but Senator Collins is estimated as being more conservative than Senator Manchin.

[6] Mitch McConnell is on this list for procedural reasons: he frequently votes “with” the Democrats on cloture motions when it is clear that cloture will fail, so as to reserve the right to motion to reconsider the vote in the future.

 

This is a guest post by David Epstein. 

Picture this: you are on a committee to hire a new CEO for a large, multinational firm. There are a number of qualified candidates, you are told, each of whom has many years of experience in the relevant field, and then you are handed a background folder on each of them. In the folder you find detailed statements of what they would like to do with the company if they are hired.

So far so good, but when it comes to the candidates’ histories, the folder talks only about their deep formative experiences from when they were children, along with some amusing anecdotes from their lives over the past few years. Nowhere, though, does it tell you how these candidates have actually performed in their professional careers. Have they been CEO’s before? If so, how did their companies do? What projects have they tackled in the past, and what were the outcomes? All excellent questions, but nothing in the files provides any answers.

This is the situation voters find themselves in every four years when choosing a president. They are told what policies the candidates promise to enact if elected, sometimes with an evaluation of how realistic and/or desirable those policies would be. But nowhere, for the most part, are they given the candidates’ backgrounds in jobs similar to the one they are running for. (An outstanding exception to this rule is Vox’s review of Marco Rubio’s tenure as Speaker of the Florida House of Representatives.)

The Task Ahead

Here, I will begin to remedy this gap by comparing the legislative records of the four candidates who have spent time in the Senate: Sanders, Clinton, Rubio and Cruz. Sanders has proposed a “revolutionary” set of reforms; how likely is he to be able to make them into policy? Clinton spent twice as long as a senator from New York than as Secretary of State, but somehow that chapter in her political history is rarely spoken about. Rubio and Cruz are newer to the Senate, Rubio more of an establishment legislative figure (at least at first), and Cruz more clearly ideological. Do either of them have histories of getting their policies passed? And yes, it’s true – Rubio and Cruz have now dropped out of the race. But a) they might still be on the ballot as VP candidates, and b) it is interesting to compare them with the Democrats, as explained below.

Now, no one set of measures can completely capture how well a legislator does their job. I’ll be examining statistics having to do with proposing, voting on, and passing legislation, which might be considered legislators’ core activities. But members of Congress also must spend time doing constituency service, sitting on committees and subcommittees, appearing in the media, and more. And, of course, what of the candidates who were executives (governors) previously — how should we measure their performance? This analysis isn’t meant to be the final word on the subject; rather, it should provide some interesting material to consider and, hopefully, open a wider discussion on assessing candidates’ qualifications for the presidency.

TL;DR: Clinton comes out looking good in terms of effectiveness and bipartisan cooperation, and Rubio does surprisingly well for his first term, sliding down after that. Sanders had a burst of activity from 2013-14, but his years before and after that aren’t very impressive. Cruz’s brief time in the Senate has been almost completely unencumbered by working to pass actual legislation.

Left-Right Voting Records

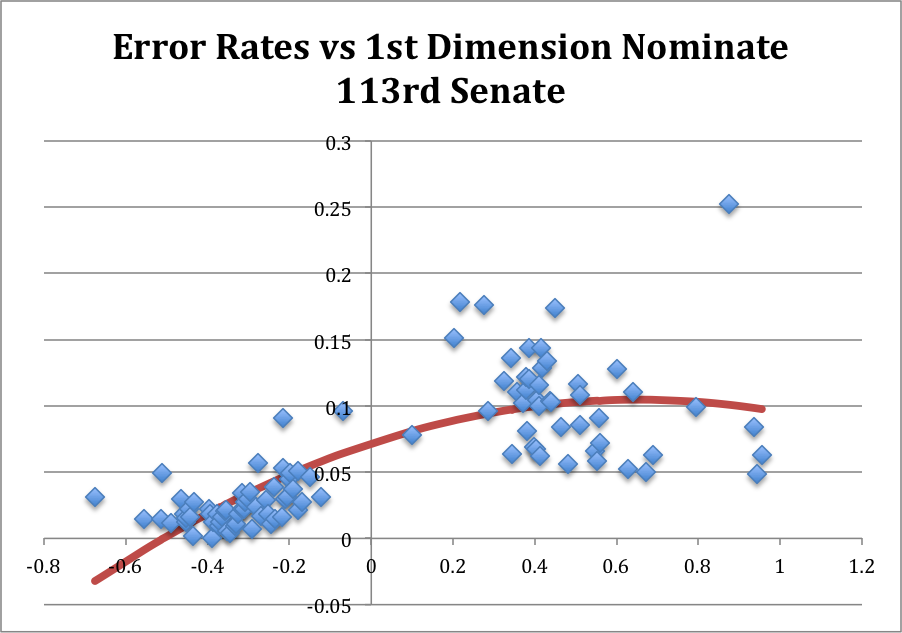
Let’s start by looking at how liberal/conservative the candidates’ voting patterns were while in office. Political scientists have developed a scale for measuring the left-right dimension of voting, called the Nominate score. I ranked these scores by Congress, with 1 indicating the senator with the most liberal voting record, and 100 being the most conservative. [NB: Each Congress lasts two years, with the 1st going from 1789-1790, and so on from there. For our purposes, the relevant Congresses stretch from the 107th (2001-02) to the current 114th Congress (2015-16). Since the 114th isn’t over yet, its statistics should be correspondingly discounted relative to the others.]

As shown in the table below, the four candidates form almost perfectly symmetric mirror images of each other. Clinton was around number 15 during her four terms in the Senate, while Rubio was 85. So each of them, despite being tagged as the “establishment” or “moderate” candidates in the primaries, was each more extreme than the average member of their own parties. That is, Clinton voted in a reliably liberal direction, even more so than the majority of her Democratic colleagues, while the same holds true for Rubio vis-à-vis the Republican senators.

Congress	State	Name	Rank
107	NEW YORK	CLINTON	14
108	NEW YORK	CLINTON	15
109	NEW YORK	CLINTON	13
110	VERMONT	SANDERS	1
110	NEW YORK	CLINTON	15
111	VERMONT	SANDERS	1
112	VERMONT	SANDERS	1
112	FLORIDA	RUBIO	85
113	VERMONT	SANDERS	1
113	FLORIDA	RUBIO	86
113	TEXAS	CRUZ	100

The Candidates, Ranked by the “Liberalness” of their Senate Voting
(1: Most Liberal, 100: Most Conservative)

Sanders and Cruz also form a perfect pair of antipodes. Sanders had the most liberal voting record for each of his terms, while Cruz was the most conservative. As a note: the only time that a party’s nominee had the most extreme voting record in their party was George McGovern in 1972 –- draw your own conclusions.

The symmetry is broken, however, when you consider the states the candidates represent(ed). Vermont is by many opinion poll measures the most liberal state in the country, and Clinton’s rank almost perfectly reflects New York’s relative position as well. Cruz and Rubio, on the other hand, have voting records considerably more conservative than Texas (number 33 out of 50 in conservative opinions of its voters) or Florida (number 23 out of 50) residents, respectively.

Bill Passage

Voting analysis can give us clues to the kind of policies a president might pursue in office. But can they get legislation passed? The next two figures show the number of bills and amendments introduced by each candidate, and the number of those that eventually passed into law, along with the overall average for each Congress.

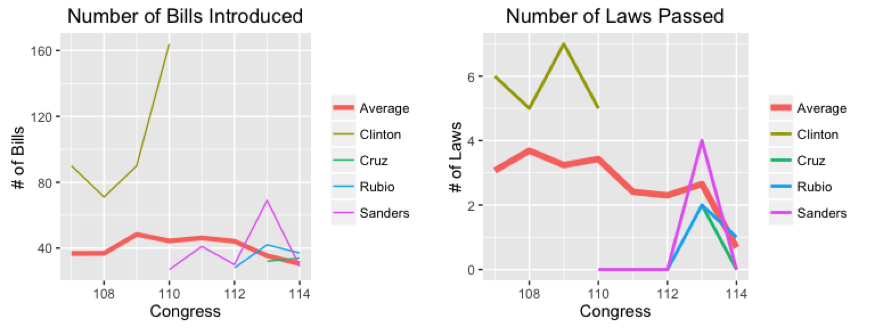
Note first that, although the average number of bills introduced has stayed more or less constant over time, the number actually passed has taken a nosedive in recent years. This reflects the increased partisan divisions in Congress, as well as the electorate, that have made Obama’s second term one where policy change may happen via executive actions or rulings in important Supreme Court cases, but rarely via the normal legislative route.

In terms of the various candidates, Clinton was by far the most active in terms of introducing and passing legislation; her totals are significantly above congressional averages for each of her terms in office. This makes sense in terms of her political history: Clinton entered the Senate in 2001 with a lot to prove — she had won just 15 of New York’s 62 counties in her 2000 election victory and wanted to establish herself as a legislator who could get things done. She worked hard, especially pushing programs that benefitted upstate New York’s more rural, agricultural economy, and was rewarded in 2006, winning re-election handily with a majority in 58 counties.

Sanders, on the other hand, has fewer legislative achievements to his name. He had a spurt of activity in the 113th Congress (2013-14), where, perhaps looking forward to his upcoming presidential bid, he introduced 69 measures, four of which passed into law. As noted above, Sanders has consistently represented his state’s liberal voters, but while the policies he has proposed may have been popular at home, in general they have not won sufficient support to be enacted into law.

Cruz and Rubio are about average in terms of measures introduced and below average for number passed. Neither, to date, has a major legislative initiative to their name. But see the next section, for Rubio’s record has more to it than it seems.

Co-Sponsorship

Actually passing policy means getting others to support your positions, and in today’s environment that entails getting members of the opposite party to vote in favor of your proposals, at least every once in a while.

Thus we now turn to analysis of cosponsorship trends. When a bill or amendment is introduced by a member of Congress — making them the “sponsor” of that measure — other members of their chamber can register their support for it by adding themselves as “co-sponsors.”

As the figure below shows, even though Clinton was far ahead of the others in terms of getting her bills passed into law, she did not have an especially high number of cosponsors per bill, on average. Neither did any of the other candidates, with the notable exception of Rubio in his first few Congresses.

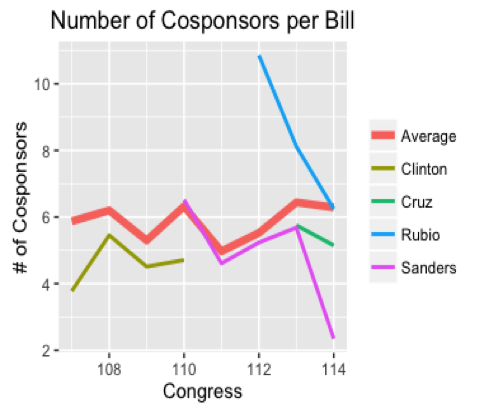
As the chart shows, the few measures that he introduced in his first years in office were relatively high-profile, gaining the support of a number of colleagues. However, the efforts produced few results, one example being the immigration reform bill he introduced as a member of the bipartisan “gang of eight” after the 2012 elections. Thus Rubio’s time in the Senate — somewhat similar to his presidential campaign — started out with a flurry of activity but then faded out, as he failed to assemble coalitions to get behind his proposals.

To measure the candidates’ track records of creating bipartisan coalitions, we look at two measures of their ability to attract the support of their colleagues from across the aisle. First, the percent of cosponsors who come from the opposite party. Second, a measure of “cosponsor coverage,” meaning the number of senators who cosponsored at least one measure proposed by the given candidate in the course of a single Congress.

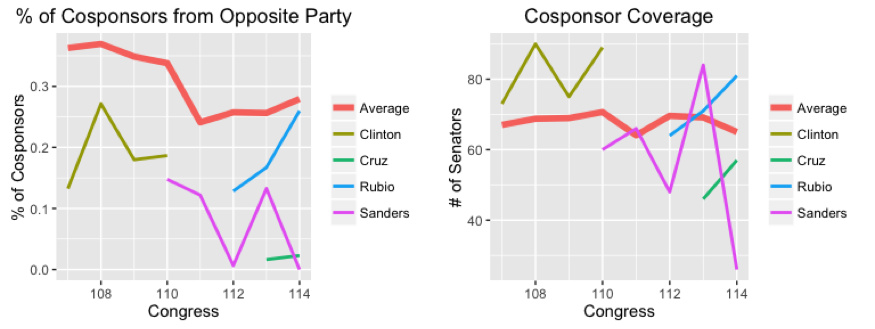
All of the candidates perform a bit below average in the percent of cosponsors from the opposite part, with Clinton and Rubio again doing better than Sanders or Cruz. And in the coverage measure, Clinton is relatively high, with Sanders and Rubio close on her heels (except for the most recent Congress, where Sanders has almost no cosponsors for the measures that he has introduced). Cruz is especially low in coverage, gaining three Democratic supporters in his first term, and four in this, his second term. Of course, Cruz has spent his time in the Senate mainly working to oppose existing policies (via government shutdowns and filibusters) rather than create new ones, so this is not too surprising.

Conclusions

Of course, there has been one other sitting senator — the first since John F. Kennedy in 1960 — elected to the presidency, and that is Obama, who spend four years in the Senate prior to his election in 2008. (Nixon spent two years in the Senate before becoming Eisenhower’s VP, and Lyndon Johnson was a senator when he became Kennedy’s VP.) What would this analysis have said about him?

Obama’s voting record was a tad more conservative than Clinton’s — number 18 on the list compared to her 15 — but he also represented a slightly less liberal state than she did. He proposed an average of 68.5 bills each Congress, which is higher than average, but he only passed a below-average 1.5 bills per Congress. Thus Obama had a lot of ideas about what to do, but didn’t yet have the track record of being able to work with his fellow senators to bring these ideas to fruition.

Interestingly, Obama’s bipartisan measures are all average or above average compared to the other candidates, so while trying to garner support for his bills he was able to work with Republicans fairly well. This would probably have made it even more of a surprise when, once he took office, the Republican party as a whole refused to work with him in any fashion to pass his policy agenda.

The Democratic and Republican Parties each use a weighted voting system to choose their presidential nominees.  This only matters when no candidate has a majority of the delegates, and the details are complicated because the weight a particular candidate has is actually a number of (possibly independent) delegates.  Leaving those details to the side, let’s consider how much Donald Trump’s wins on Tuesday April 26th “mattered.”  The simplest measure of success, for each candidate, is how many additional delegates they each won.  As a result of Tuesday’s primaries, Trump is estimated to have picked up 110 delegates, Senator Cruz is estimated to have picked up 3, and Governor Kasich similarly is estimated to have picked up 5.

A key concept in weighted voting games is that of power.  There are literally countless ways to measure power, but one of the most popular ways is called the Banzhaf index.

If there are total votes, and a candidate “controls” of those votes, the Banzhaf index measures the probability, given the distribution of the other  votes across the other candidates, that the candidate in question will cast the decisive vote: that is, that he or she will have enough votes to pick the winner, given every way the other candidates could cast their ballots. (I’m skipping some details here.  For the interested, the most important detail is that the index presumes that the other candidates will randomly choose how to vote.)

A higher power index implies that the candidate is more likely to determine the outcome. What is key is that the power index for a candidate with votes out of is generally not equal to .  For example, if a candidate has over half of the votes,[1] then that candidate’s Banzhaf index is equal to 1 (and those of all other candidates are equal to zero, and we’ll see that come up again below), because that candidate will always cast the decisive vote.

So, back to Tuesday.  Here is the breakdown of how the GOP candidates’ delegates translated into “Banzhaf power” before Tuesday’s primaries.

Candidate	Donald Trump	Ted Cruz	John Kasich	Marco Rubio	Ben Carson	Jeb Bush	Carly Fiorina	Rand Paul	Mike Huckabee	Total
Delegates	846 (48.85%)	548 (31.64%)	149 (8.6%)	173 (9.99%)	9 (0.52%)	4 (0.23%)	1 (0.06%)	1 (0.06%)	1 (0.06%)	1,732
Banzhaf Power	0.5	0.1667	0.1667	0.1667	0.1667	0	0	0	0

Going into Tuesday’s primaries, Trump held just under majority of the delegates and held exactly half of the power.  More interesting in this comparison is that Marco Rubio’s power was still significant: in fact, equal to the individual powers of Kasich and Cruz.

Even though Rubio and Kasich each had less than a third of Cruz’s delegates, their voting power as of Monday was equal to Cruz’s. This is due to the fact that Rubio, Kasich, and Cruz could defeat Trump if and only their delegates voted together, regardless of how the other delegate-controlling candidates had their candidates vote.  In other words, Carson, Bush, Fiorina, Paul, and Huckabee truly had—as of Monday (and today)—no bargaining power at a contested convention.

However, after Tuesday’s results, the following happened:

Candidates	Donald Trump	Ted Cruz	John Kasich	Marco Rubio	Ben Carson	Jeb Bush	Carly Fiorina	Rand Paul	Mike Huckabee	Total
Delegates	956 (51.68%)	551 (29.78%)	154 (8.32%)	173 (9.35%)	9 (0.49%)	4 (0.22%)	1 (0.05%)	1 (0.05%)	1 (0.05%)	1,850
Banzhaf Power	1	0	0	0	0	0	0	0	0

By securing a majority of the delegates allocated so far, Trump’s power jumped from 0.5 to 1 and all of his opponents’ powers dropped to zero.  If the convention occurred today, they would be powerless to stop Trump.

Now, suppose that the candidates had votes equal to the actual votes (rather than delegates) they receive.  If the convention were held today under such rules, this would result in the following:

Candidates	Donald Trump	Ted Cruz	John Kasich	Marco Rubio	Ben Carson	Jeb Bush	Jim Gilmore	Chris Christie	Carly Fiorina	Rand Paul	Mike Huckabee	Rick Santorum	Total
Popular Votes	10,121,996 (39.65%)	6,919,935 (27.10%)	3,677,459 (14.40%)	3,490,748 (13.67%)	722,400 (2.83%)	270,430 (1.06%)	2,901 (0.01%)	55,255 (0.22%)	36,895 (0.14%)	60,587 (0.24%)	49,545 (0.19%)	16,929 (0.07%)	25,530,125
Banzhaf Power	0.5	0.1667	0.1667	0.1667	0	0	0	0	0	0	0	0

If the popular votes were the basis of the GOP nomination and the convention were held today, then the candidates would still have the same “powers” as they did prior to Tuesday’s primaries.  Thus, on Tuesday, we arguably truly witnessed the effect of the “delegate system.”

As a final note, this power calculation clearly indicates something that I think is underappreciated about multicandidate races in majority rule settings.  To break Trump’s lock on the race, it is unimportant which candidate (other than Trump) an “unpledged” delegate decides to support.  Right now, if and only if at least 62 unpledged delegates (and I have no idea how many of them there are left right now) decide to support “other than Trump,” then the Trump’s power drops below.  In addition to (and in line with) the fact that it doesn’t matter how those delegates allocate their support across the other candidates, if 62 such delegates appeared in the hypothetical conference tomorrow in Cleveland, the powers of the candidates would be as follows:

Candidates	Donald Trump	Ted Cruz	John Kasich	Marco Rubio	Ben Carson	Jeb Bush	Carly Fiorina	Rand Paul	Mike Huckabee	Total
Delegates	956 (50%)	613 (32.06%)	154 (8.05%)	173 (9.05%)	9 (0.47%)	4 (0.21%)	1 (0.05%)	1 (0.05%)	1 (0.05%)	1,912
Banzhaf Power	0.97	0.004	0.004	0.004	0.004	0.004	0.004	0.004	0.004

Conclusion. There are two “math of politics” points in here. The first is that votes/delegates are definitely not a one-to-one match: indirect democracy is distinct from direct democracy—it’s always important to remember that.  The second, and more “math-y” is that, when people have different numbers of votes, it is not the case that the number of votes a person has is equal to his or her voting power.[2]

With that, I leave you with this.

PS: If you would like (Mathematica) code to calculate the Banzhaf index for this and other situations, email me.

___________

[1] I am assuming for simplicity throughout, in line with the rules of the GOP and Democratic Party, that the collective decision is made by simple majority rule.  One can calculate the Banzhaf index for any supermajority requirement as well.  As the supermajority requirement goes up, the power indices of all candidates with a positive number of votes converge to equality (guaranteed to occur when the decision rule is unanimity).

[2] For a great review of how this is important in the real world, see Grofman and Scarrow (1981), who discuss a real-world use of weighted voting in New York State back in the 1970s.

I posted earlier about truels and how the current GOP nomination approximates one.  In that post, I laid out the basics of the simple truel (i.e., a three person duel), assuming that the three shooters shoot sequentially.  Things can be different when the three shooters shoot simultaneously.[1]  Short version: Trump and Rubio aren’t allies, but game theory suggests they should both attack Cruz, in spite of this.

This is arguably a better model for debates than the sequential version, in which candidates prepare extensively prior to debate, largely in ignorance of the other debaters’ preparations. Leaving that interesting question aside, let’s work this out.  I assume that the truel lasts until only one shooter is left, and that each shooter wants to live, and is otherwise indifferent.  I’ll also assume that the best shooter hits with certainty.[2] The probability that the second-best shooter hits his or her target is 0<p<1 and the probability that the worst shooter hit his or her target is 0<q<p.

When there are two shooters left, each will shoot at the other.  Not interesting, but important, because this implies that the worst shooter wants to shoot at the best shooter in the first round. In the first round, both the second-best and worst shooters shoot at the best shooter.  Either the first best or second best shooter will be dead after this (if the second-best and worst shooter each get to shoot before the first best shooter, but miss, then the second-best shooter will be killed with certainty). There is also a chance that the worst shooter will win in the first round: the best shooter kills the second-best shooter (probability 1/3), and the worst shooter kills the best shooter (probability q<1).

What does this say about the GOP race?  Both Rubio and Trump should be shooting at Cruz.  This is a simplistic model, and it ignores a lot of real-world factors.  But that’s why it’s valuable, from a social science perspective: if (and when) the behaviors of the three campaigns deviate from this behavior, we know that we need to include those other factors.  Until then, you see, in this world there’s two kinds of models, my friend: Those with just enough to capture the logic and those who need to dig for more things to include.  We’ll see if this one needs to dig.

With that, I leave you with this.

____________________

[1]. For simplicity, I will assume that, if two shooters shoot at each other, then one of them, randomly chosen, will “shoot first” and, if he or she kits, kill the other shooter before he or she fires his or her weapon.  Note that, with this assumption, if shooter A knows that shooter B (and only shooter B) is going to shoot at shooter A, then shooter A should definitely shoot at shooter B.

[2]This assumption isn’t as strong as it appears. This is because the truel is already assumed to continue until only one player is left (note that it is impossible for zero shooters to survive, given the tie-breaking assumption).

A truel is a three person duel.  There are lots of ways to play this type of thing, but the basic idea is this: three people must each choose which of the other two to try to kill.  They could shoot simultaneously or in sequence.  The details matter…a lot.  I won’t get into the weeds on this, but let’s think about the GOP race following last night’s Iowa caucus results.  By any reasonable accounting, there are three candidates truly standing: Ted Cruz, Marco Rubio, and Donald Trump.  The three of them took, in approximately equal shares, around 75% of the votes cast in the GOP caucus.

The next event is the New Hampshire primary, and the latest polls (all conducted before the Iowa caucus results) have Trump with a commanding lead and Rubio and Cruz essentially tied for (a distant) second.  So, the stage is set.  Who shoots first?  And at whom?

The truel is a useful thought experiment to worm one’s way into the vagaries of this kind of calculus.  A difference between truels and electoral politics is that the key factor in a standard truel is each combatant’s marksmanship, or the probability that he or she will kill an opponent he or she shoots at.  What we typically measure about a candidate is how many survey respondents support him or her.  For the purposes of this post, let’s equate the two.  Trump is the leader, and Rubio and Cruz are about equal.

A relatively robust finding about truels is that, when the shots are fired sequentially (i.e., the combatants take turns), each combatant should fire at the best marksman, regardless of what the other combatants are doing (this is known as a “dominant strategy” in game theory).  Thus, if we think that the campaigns are essentially taking turns (maybe as somewhat randomly awarded by the vagaries of the news cycle and external events), then both Rubio and Cruz should be “shooting at Trump.”  This is in line with Cruz’s post-caucus speech in Iowa last night.

An oddity of this formulation of the truel is that it is possible that the best marksman is the least likely to survive.  This is true even if the best marksman gets to shoot first.

Is it current, or future, popularity? An alternative measurement of marksmanship, however, is not the current support, but the perceived direction of change in support.  After all, marksmanship is about the ability to kill someone on the next shot.

On this front, Rubio is currently the better marksman: his support in Iowa vastly exceeded expectations, while by many accounts (though not necessarily my own), Trump is the worst marksman.  If one buys this alternative measure, then the smart strategy for both Trump and Cruz is to “aim their guns” at Rubio.  We have a week to see who they each aim at.

Of course, a truel is a simplistic picture of what’s going on in the GOP nomination process. In reality, it is probably better to think that each candidate’s marksmanship depends on his (or her) choice of target.  Evidence suggests that it is harder for Trump to “shoot down” Cruz than it was for him to shoot down Bush.  Maybe I’ll come to that later.  For now, I’m still making sense of Santorum’s strategy of heading to South Carolina. For that matter, I’m trying to make sense of him being called “a candidate for President.”

With that, I leave you with this.

This is math, but it isn’t politics.  This is serious business.  This is the NFL.

The New England Patriots won the coin toss to begin today’s AFC championship game against the Denver Broncos. With that, the Patriots have won 28 out of their last 38 coin tosses. To flip a fair coin 38 times and have (say) “Heads” come up 28 or more times is an astonishingly rare event. Formally, the probability of winning 28 or more times out of 38 tries when using a fair coin is 0.00254882, or a little better than “1 in 400” odds.

But the occurrence of something this unusual is not actually that unusual. This is because of selective attention: we (or, in this case, sports journalists like the Boston Globe‘s Jim McBride) look for unusual things to comment and reflect upon. I decided to see how frequently in a run of 320 coin flips a “window” of 38 coin flips would come up “Heads” 28 or more times. I simulated 10,000 runs of 320 coin flips and then calculated how many of the 283 “windows of 38” in each run contained at least 28 occurrences of “Heads.” (For a similar analysis following McBride’s article, considering 25 game windows, see this nice post by Harrison Chase.)

The result? 441 runs: 4.41%, or a little better than “1 in 25” odds. (Also, note that the result would be doubled if one thinks that we would also be just as quick to notice that the Patriots had lost 28 out of the last 38 coin tosses.)

The distribution of “how many windows of 38” had at least 28 Heads, among those that contained at least one such window, is displayed in the figure below. (I omitted the 9,559 runs in which no such window occurred in order to make the figure more readable.)

 

Accounting for correlation. Inspired partly by Harrison Chase’s post linked to above, I ran a simulation in which 32 teams each “flipped against each other” exactly once (so each team flips 31 times), and looked at the maximum number of flips won by any team. This relaxes the assumption of independence used in both the first simulation and, as noted by Chase, the Harvard Sports Analysis Collective analysis linked to above. I ran this simulation 10,000 times as well. I counted how many times the maximum number of flips won equaled or exceeded 23, which is the number of times the Patriots won in their first 31 games of the current 38 game window (i.e., through their December 6^th, 2015 game against the Eagles).

The result? In 1,641 trials (16.41%), at least one team won the coin flip at least 23 times.

The Effect of Dependence. Intuition suggests that accounting for the lack of independence between teams’ totals decreases the probability of observing runs like the Patriots’. To see the intuition, consider the probability two teams both win their independent coin flips: 25%, and then consider the probability both teams “win” a single coin flip: 0%.

My simulations bear out this intuition, but the effect is bigger than I suspected it would be. Running the same 10,000 simulations assuming independence, at least one team won the coin flip at least 23 times in 2,763 trials (27.63%).

The histograms for the maximum number of wins in each of the 10,000 simulations, first for the “team versus team dependent” case and the second for the “independent across teams” case, are displayed below.

 

Takeaway Message.  Of course, anything that occurs around 5% of the time is not an incredibly common occurrence, but it illustrates that, it’s not that unusual for something unusual to occur. For example, note that the NFC once won the Super Bowl coin toss 14 times in a row (Super Bowls XXXII to XLV), an event that occurs with probability 0.00012207, or a little worse than “1 in 8000” odds. And, of course, we recently saw a coin flip in which the coin didn’t flip.

An empirical matter: somebody should go collect the coin flip data for all teams.  One point here is that looking at one team probably makes this seem more unusual, and the first intuition about the math might suggest that we can simply gaze in awe at how weird this is.  But, upon reflection, we should remember that we often stop to look at weird things without noting exactly how weird they are.

____________________________

Notes.

1. The probability 0.00254882 in the introduction is obtained by calculating the CDF of the Binomial[38,0.5] distribution at 27, and then subtracting this number from 1.  A common mistake (or, at least, made by me at first) is to calculate the Binomial[38,0.5] distribution at 28 and subtract this number from 1. Because the Binomial is an integer valued distribution, that actually gives the probability that a coin would come up Heads at least 29 times. The difference is small, but not negligible, particularly for the point of this post (considering the probability of a pretty rare event occurring in multiple trials).
2. 320 flips is 20 years of regular season games. Not that the streak is constrained to regular season games. I like Chase Harrison’s number (247, the number of games Belichick had coached the Patriots at the time of his post) better, but I didn’t want to re-run the simulations.
3. The probability of this “notable” event is even higher if one thinks that the we would be paying attention to the event even if the Patriots had won only (say) 27 of the last 38 flips.
4. I did the simulations in Mathematica, and the code is available here.

In response to the concerns raised by colleagues (principally and initially in this petition, but see also Chris Blattman’s take and other responses from both sides), I wanted to clarify why I think that delaying implementation of the Journal Editors’ Transparency Statement (JETS) is a poorly thought out goal, one that will differentially disadvantage some scholars, particularly younger, less well-known scholars.

These Standards Are Already Being Implemented. To begin, and reiterate one of the arguments I made here a few days ago, journal editors already have the unilateral discretion to impose the kinds of policies that JETS is calling upon editors to implement. To wit, editors are already implementing policies along these lines. For example, see the submission/replication guidelines of the American Journal of Political Science, American Political Science Review, and the Journal of Politics, to name only three. These three vary in details, but they are consistent with JETS as they stand right now.

It’s Happening Anyway, Let’s Stay In Front of It.  The point is that the JETS implementation is already under way and, indeed, was underway prior to the drafting of JETS. The DA-RT initiative is simply providing a public good: a forum for exactly the conversations that the petition signers seek. (The individuals who have contributed time to the public good that is DA-RT, and their contributions, are described here.)

The Clarifying Quality of Deadlines. The “implementation of JETS” scheduled for January 2016 is best viewed as a moment of public recognition that we as a discipline need to continue the conversations. Editorial policies are not written in stone, after all. Thus I strongly believe that delaying the implementation of JETS will do nothing other than further muddy the waters for scholars. JETS is about recognizing and shepherding the movement towards more coherent and uniform procedures to increase the transparency of social science research. Delaying it will place scholars, particularly junior and less well-known scholars, at a disadvantage. This is because implementation of the JETS will give all scholars firmer ground to stand on when seeking clarification of the details of a journal’s replication and transparency requirements.

Clear Policies Level the Playing Field and Make Editors (more) Accountable. Furthermore, scholars will be able to publicly compare and contrast these procedures, allowing more judicious selection of research design, early preparation of justifications for requests for exemptions, and finally, a counterpoint for an editorial decision that is inconsistent with the standards of peer outlets. That is, if journal X decides that one’s research is sufficiently transparent and then journal Y decides otherwise, the transparency of those journals’ standards—which JETS aims to ensure are publicly available—will ensure that the journals’ standards are fair game for comparison and debate. This is the type of conversation sought by many of the petition signers I have spoken with. Implementation of JETS will push this conversation forward, whereas delay will simply retain the status quo of an incoherent bundle of idiosyncratic policies.

Will The Sun Rise on January 15, 2016? It is important to keep in mind that the implementation of the JETS statement will in most cases result in no new policy: journal editors have been setting and fine-tuning standards like these for decades. Rather, implementing JETS binds editors—like myself—more closely to the sought-after conversations about how best to achieve transparency in the various subfields and with respect to the various methodologies of our discipline.

In other words, implementation of JETS will empower scholars to demand more transparency and accountability from the editors of the 27 journals that have signed the statement.

With that, I leave you with this.

Hey, long time no see. While we’ve been apart, there’s arisen a bit of a dustup in my little corner of the world about the Data Access and Research Transparency (DA-RT) initiative. In a nutshell, DA-RT represents a movement to continued discussion, implementation, and fine-tuning of standards regarding how social science research is produced and shared amongst scholars and the broader community.

In (quite belated) response, this petition dated November 3rd, 2015, requests a delay in the implementation of “DA-RT until more widespread consultation can be accomplished at, for instance, the regional meetings this year, and the organized section meetings and panels and workshops at the 2016 annual meeting.”

With the background set, a disclosure/explanation is in order: I am a coeditor of the Journal of Theoretical Politics, and hence a co-signatory on the DA-RT Journal Editors’ Transparency Statement (JETS).  That’s basically why I’m writing this, particularly once one reads the petition twice and realizes that, its length and detail notwithstanding, it is entirely unclear to whom the petition is directed (other than “colleagues”).

In practical terms, is this a petition to

1. Journal editors?
2. Journal publishers?
3. Journals’ editorial boards?
4. Journal reviewers?
5. The governing bodies of the various political science associations?
6. Political scientists in general?

In the spirit of this blog and my own view of the world, I’ll be clear:

the absence of a clearly named target of the petition is absolutely and definitively telling: this is not a serious (or at least well thought-out) plea. Full. stop.

Delay, delay, delay.  Without impugning any of the signers of the petition, it is clear to me that the petition is classic and barely disguised foot-dragging. This petition, as drafted, will do nothing to further serious dialogue about the issues at hand. Rather, it draws a (sadly, frequently and unnecessarily drawn) line in the sand between quantitative and qualitative analyses in the social sciences.

Transparency is hard for everybody.  The petition states that “Achieving transparency in analytic procedures may be relatively straightforward for quantitative methods executed via software code.” Sure, it might be. But it need not be. Difficulties with implementing transparency are qualitatively common to all forms of analysis: formal, quantitative, and qualitative. Formal analysis can depend on methods, proofs, or arguments that are obscure or opaque even to many scholars. Along the same lines, both quantitative and qualitative methods can be difficult to convey in a parsimonious fashion. Finally, both quantitative and qualitative analyses can bring up questions about how to preserve anonymity of subjects, maintain incentives for the collection of new data (“embargoing”), etc.

Let’s keep talking…at, you know, some place and some time. Each of the above issues is difficult to deal with, of course. But rather than acknowledging this (clear) reality and putting something productive forward, the petition instead suggests that “we” should delay implementation

 “until more widespread consultation can be accomplished at, for instance, the regional meetings this year, and the organized section meetings and panels and workshops at the 2016 annual meeting. Postponing the date of implementation will allow a discipline-wide consideration of the principles of data access and research transparency and how they should be put into practice.”

 

To understand why this is foot-dragging, note first this “Response by the DA-RT organizers to Discussions and Debates at the 2015 APSA Meeting” (henceforth “the Response”). Seriously, if you’re already here in this post, you should take the time to read it. It’s not that long, but it’s got a lot of information.

Finished reading it?  Good.  Let’s move on to what I think is the money shot of the Response, and it’s adroitly situated right in the opening:

At the 2015 Annual Meeting of the American Political Science Association in San Francisco, DA-RT and JETS were a central topic at several meetings. There were multiple workshops, roundtables, and ad hoc discussions. In addition, transparency was debated at several of the organized section business meetings. As a result, conversations about openness took place on almost every day of the Annual Meeting. As facilitators of a now five-year long dialogue on openness, we were of course delighted that the topic received such a wide airing. (Emphasis added and doubled.)

 

All that said, the petition asks for more discussions: “discussions” that are neither organized nor even clearly described. Just a vague call for “let’s talk some more at some of those meetings that we’ll all be at in the next year or so.”

But, wait…to stop piling on and return to the facts as stipulated by both the Response and the petition itself: such discussions have been going on for the past 5 years. 

Yes, it’s tough.  But the sky isn’t falling.  Look, both sides of the debate are filled by smart and well-meaning scholars.  Is the topic at hand—implementing the right kind(s) of transparency in research—a hard task?     Yes.    …And all involved acknowledge that, even if only because denying it would be ridiculous.

Any Good Transparency Standard Requires and Relies Upon Context. Why is this a hard task? Because there’s no perfect answer. Transparency is a beguiling concept, especially to scholars. To beguile implies at least a strong possibility of deception (which is ironic) and the allure of transparency fits this bill, precisely because “transparency” is like obscenity: you know it when you see it, because when you see it, you can account for the context. If a statue of a nude person is made of marble, it’s totally okay: not obscene. If you withhold data because the IRB (or contract, law) requires you to do so, or because revealing it would put people in harm’s way, that’s okay: still transparent. Just tell the editor(s) and reviewers (and, by extension) readers why.  This is a collaborative enterprise, this search for knowledge and betterment.  In the end, we’re in this together.

Look, This Ain’t A Democracy.  Finally, and I think most importantly, note that editors can and do impose policies about topics like this. Simply put, the petition is silly because journals and their editors do (and should) have discretion: that’s why we don’t have one big “JOURNAL OF RESEARCH” that everybody publishes in.

More specifically, and as the Response states,

It is important to note that JETS does not create new powers for journal editors. Instead, it asks them to clarify or articulate decisions they are already making or attempting to manage. Journal editors have had, and will continue to have, broad discretion to choose what they will and will not publish and their basis for doing so. (Emphasis added…twice.)

 

This isn’t about quantitative versus qualitative.  The petition draws a false, and all too commonly drawn, line in the sand.  The Response—and clear thinking—makes clear that neither the issue of transparency nor reproducibility differentially impinges on scholars due to the nature of their data or their method.  Data is data, method is method.  Sure, the implementation details of how best to achieve transparency will vary from one study to another—but this is based on the subject, not the nature of the data or method.  A method is something that can be done…you know…methodically.  That doesn’t require numbers.  Write down your method.  Share your data to degree that is legally and ethically possible.  Stop being fearful.  If none of that works, ask the editor for an exception.  If all of those steps fail…publish it somewhere else.  You can be like John Fogerty, Trent Reznor, or Prince.

This petition is cynical.  In the end, there’s no fire in that barn: somebody else is just blowing a lot of smoke from behind it. The petition is a manipulative force both playing upon and probably driven by fear.  Hopefully either the Response or maybe even even this post makes clear that this fear is unwarranted.

In the end, “haters gonna hate,” and, as a corollary, “editors gonna reject.”

Neither the DA-RT initiative, nor the petition, will change either of those truisms.

With that, I leave you with this.