I have been thinking a lot lately about this very interesting post by Kristina Lerman. The post is excellent: succinct and well-written, data-centric, and relevant beyond the data’s idiosyncratic qualities. In a nutshell, Lerman’s central question is whether the rate of information production is outstripping the rate at which we (choose to or can) consume and digest it.
Of course, information overload is clearly an important problem for scholars and practitioners alike (and, accordingly, not one with any obvious and easy answer). But upon reflection, I am still wondering whether it is a problem at all. Given my second-mover advantage, I will cherry-pick one of the arguments in the post.
In a section titled “Rising Inequality,” Lerman uses the Gini coefficient of citations to physics papers as a measure of scholarly inequality. Since the Gini coefficient has grown over the past 6 decades, Lerman concludes that “a shrinking fraction of papers is getting all the citations.” This is undoubtedly true once one slightly rewords it as “a shrinking fraction of the papers made available is getting all the citations.” This is an important qualifier, in my opinion, and the central point of this post.
Any notion of inequality is inherently relative. As I read it, Lerman’s argument is that the increase in information production has potentially caused us to use cues or heuristics to manage the decision of what information we as scholars consume. Lerman argues that this is bad because the Gini coefficient has increased along with the rate of publication, indicating that the cues and heuristics we are employing is narrowing our attention to a smaller set of articles and creating a “rich get richer” dynamic in terms of citations and scholarly focus.
However, is this conclusion warranted by the data? I am not so sure: the Gini coefficient, like any measure of inequality, is potentially sensitive in counterintuitive ways to the set of things being compared to one another.
The nature of Gini coefficients. Lerman’s argument that higher Gini coefficients are bad is very sensible if one thinks that the “pie” of citations is fixed in size and/or that the low citation articles are somehow “unjustly” receiving fewer citations. At least in my opinion, neither of these suppositions is reasonable in this context. There’s a number of ways to skin this cat, but I think this is the easiest. Suppose, for the sake of argument, that the number of citations an article will receive is independent of the number of articles uploaded (or, accepted into an APS journal). Then, suppose that only those articles that will receive m citations are uploaded. As the costs of uploading/writing/publishing decrease, m would presumably decrease as well. With this in hand, the key question is:
Holding the latent population of articles fixed, how does the Gini coefficient of the uploaded articles change as m increases?
Note that decreasing m increases the number of articles uploaded. To me, at least, Lerman’s implicit argument is that decreasing m “should” decrease inequality (i.e., decrease the Gini coefficient).
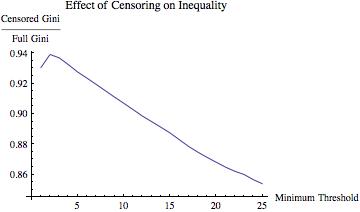
This isn’t necessarily the case. I ran a simulation to demonstrate this with a very large set of “pseudo-data.” Specifically, I generated 100,000 observations from a Pareto(k=1,
The results are displayed below
The simulated data demonstrate that increasing the selectivity of the upload/publication process can actually decrease inequality among the (changing set of) uploaded/published papers. In other words, increasing the rate of uploading/publication of articles can increase inequality without reference to information overload or any changes in citation behavior.
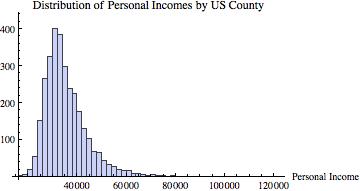
Out of curiosity, I went out and got some real data. For simplicity, I downloaded the per capita personal incomes of each US county for 2011 (available here). This data looks like this:
I then did an analogous analysis, varying the income threshold from $20,500 to $40,000, computing the ratio of the Gini of the truncated data to the Gini of the overall data set at each increment of $500. The results of this are below.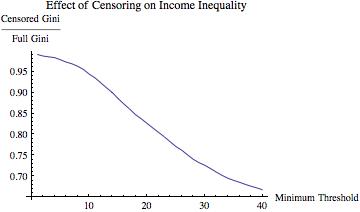
Again, as one gets more “elite” with respect to the inclusion of a county in terms of income into the calculation of the Gini coefficient, estimated inequality decreases.
Now, it is probably very simple to find examples in which the opposite conclusion holds. But that’s not the point: I am not arguing that Lerman is wrong. Rather, I am making a point about inequality measurement in general. In line with my earlier point about Simpson’s paradox and education policy, comparing relative performance between different sets-even nested ones-is tricky.*
Also, as an aside before concluding, it occurred to me that the data used by Lerman seems to vary from point to point. While the data demonstrating the rapid increase in production rate over the past two decades is from arxiv.org (and, further, note this graph, which is a more “apples-to-apples” comparison), the data on which the Gini coefficients are calculated are papers “published in the journals of the American Physical Society.” These are two very different outlets, of course: arxiv.org is not peer-reviewed, while the journals of the American Physical Society are.
While I do not have the data that Lerman is working from in her post, the difference between the two data sources might be important due to changes in the number & nature of publication outlets over the time period.
Specifically, consider either or both of the following two possibilities:
- Presumably, there are publication outlets other than the APS journals. If this is the case, even if the APS journals have published a fixed and constant number of papers per year, changing publication patterns could be far more important in determining the Gini coefficient of citations to articles published APS journals than the overall article production rate.
- After doing some poking around, I came across this candidate as the likely source of Lerman’s data for the Gini coefficient calculations. I may be wrong, of course, but if this is the data used, it considers only intra-APS journal citations. If this is the case, then one is not really looking at inequality of attention/citations broadly—just inequality within APS articles. The sorting critique from the above point applies here, too.
Conclusion: Comparisons of Inequality Are Not Always Comparable. Again, I really like Lerman’s post: this is a hard and important question. My point is only that measuring inequality, a classic aggregation/social choice problem, is inherently tricky.
With that, I leave you with this.
____________________________
* As another aside, it occurs to me that these issues are intimately related to some common misunderstandings of Ken Arrow’s independence of irrelevant alternatives axiom from social choice. But I will leave that for another post.