This is math, but it isn’t politics.  This is serious business.  This is the NFL.

The New England Patriots won the coin toss to begin today’s AFC championship game against the Denver Broncos. With that, the Patriots have won 28 out of their last 38 coin tosses. To flip a fair coin 38 times and have (say) “Heads” come up 28 or more times is an astonishingly rare event. Formally, the probability of winning 28 or more times out of 38 tries when using a fair coin is 0.00254882, or a little better than “1 in 400” odds.

But the occurrence of something this unusual is not actually that unusual. This is because of selective attention: we (or, in this case, sports journalists like the Boston Globe‘s Jim McBride) look for unusual things to comment and reflect upon. I decided to see how frequently in a run of 320 coin flips a “window” of 38 coin flips would come up “Heads” 28 or more times. I simulated 10,000 runs of 320 coin flips and then calculated how many of the 283 “windows of 38” in each run contained at least 28 occurrences of “Heads.” (For a similar analysis following McBride’s article, considering 25 game windows, see this nice post by Harrison Chase.)

The result? 441 runs: 4.41%, or a little better than “1 in 25” odds. (Also, note that the result would be doubled if one thinks that we would also be just as quick to notice that the Patriots had lost 28 out of the last 38 coin tosses.)

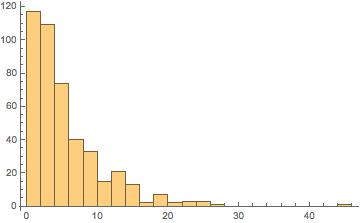
The distribution of “how many windows of 38” had at least 28 Heads, among those that contained at least one such window, is displayed in the figure below. (I omitted the 9,559 runs in which no such window occurred in order to make the figure more readable.)

Figure 1: How Many Windows of 38 Had At Least 28 Heads

Accounting for correlation. Inspired partly by Harrison Chase’s post linked to above, I ran a simulation in which 32 teams each “flipped against each other” exactly once (so each team flips 31 times), and looked at the maximum number of flips won by any team. This relaxes the assumption of independence used in both the first simulation and, as noted by Chase, the Harvard Sports Analysis Collective analysis linked to above. I ran this simulation 10,000 times as well. I counted how many times the maximum number of flips won equaled or exceeded 23, which is the number of times the Patriots won in their first 31 games of the current 38 game window (i.e., through their December 6^th, 2015 game against the Eagles).

The result? In 1,641 trials (16.41%), at least one team won the coin flip at least 23 times.

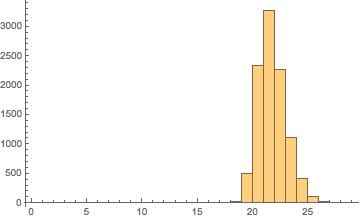
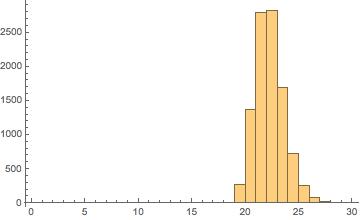
The Effect of Dependence. Intuition suggests that accounting for the lack of independence between teams’ totals decreases the probability of observing runs like the Patriots’. To see the intuition, consider the probability two teams both win their independent coin flips: 25%, and then consider the probability both teams “win” a single coin flip: 0%.

My simulations bear out this intuition, but the effect is bigger than I suspected it would be. Running the same 10,000 simulations assuming independence, at least one team won the coin flip at least 23 times in 2,763 trials (27.63%).

The histograms for the maximum number of wins in each of the 10,000 simulations, first for the “team versus team dependent” case and the second for the “independent across teams” case, are displayed below.

Figure 2: Maximum Number of Coin Flip Wins by A Team in Round-Robin 32 Team League Season

Figure 3: Maximum Number of Wins Among 32 Teams Flipping A Coin 31 Times

Takeaway Message.  Of course, anything that occurs around 5% of the time is not an incredibly common occurrence, but it illustrates that, it’s not that unusual for something unusual to occur. For example, note that the NFC once won the Super Bowl coin toss 14 times in a row (Super Bowls XXXII to XLV), an event that occurs with probability 0.00012207, or a little worse than “1 in 8000” odds. And, of course, we recently saw a coin flip in which the coin didn’t flip.

An empirical matter: somebody should go collect the coin flip data for all teams.  One point here is that looking at one team probably makes this seem more unusual, and the first intuition about the math might suggest that we can simply gaze in awe at how weird this is.  But, upon reflection, we should remember that we often stop to look at weird things without noting exactly how weird they are.

____________________________

Notes.

1. The probability 0.00254882 in the introduction is obtained by calculating the CDF of the Binomial[38,0.5] distribution at 27, and then subtracting this number from 1.  A common mistake (or, at least, made by me at first) is to calculate the Binomial[38,0.5] distribution at 28 and subtract this number from 1. Because the Binomial is an integer valued distribution, that actually gives the probability that a coin would come up Heads at least 29 times. The difference is small, but not negligible, particularly for the point of this post (considering the probability of a pretty rare event occurring in multiple trials).
2. 320 flips is 20 years of regular season games. Not that the streak is constrained to regular season games. I like Chase Harrison’s number (247, the number of games Belichick had coached the Patriots at the time of his post) better, but I didn’t want to re-run the simulations.
3. The probability of this “notable” event is even higher if one thinks that the we would be paying attention to the event even if the Patriots had won only (say) 27 of the last 38 flips.
4. I did the simulations in Mathematica, and the code is available here.